Physical Mathematics books

reviewed by T. Nelson

athematical physics is physics with all the interesting parts removed. Most readers, unless they're mathematicians, won't care much about proofs and mathematical purity; their goal is find out how to manipulate the symbols and learn what the formulas actually “do.” Others just need a reference that's more tutorial in nature than Bronshtein and Semendyayav's Handbook of Mathematics (which is still essential) when they encounter some unfamiliar dipsy-doodle.

But there's a problem: none of them is very good. I ended up reading Cahill's book cover to cover, but found myself referring to the books by Balakrishnan and Hassani to understand what Cahill was trying to say.

Cahill

Kevin Cahill's Physical Mathematics covers basic stuff like linear algebra, Fourier series, and infinite series, then covers more advanced topics like group theory, tensors, path integrals, and functional derivatives. It's the only book with chapters on renorm­aliz­ation groups, chaos, fractals, and string theory. Its distinguishing feature is its detailed examples, some extending for four pages, illustrating the use of the formulas in physics. However, despite the glowing praise on the back cover, the text is confusingly written in places. (This supports my theory that the extravagance of the praise on the back cover is inversely proportional to how useful it is. I feel a con­spir­acy theory coming on . . . .) Some of the terms are defined tautologically, some have descriptions hidden in the text, and some aren't defined at all. For instance, on page 262 Cahill says this:

A self-adjoint differential system consists of a real formally self-adjoint operator, a differential equation on an interval, boundary conditions, and a set of twice-differentiable functions that obey them.

Compare that to Balakrishnan's Mathematical Physics:

An operator A is self-adjoint if A = A^†.

That's how it's defined in every particle physics book I've ever read, and since the reader knows by this point what A^† means it's immediately clear. Cahill's discussion meanders about boundary conditions, Legendre's system, and Wronskians. Meanwhile, Balak­rish­nan tells us explicitly what it means and why we have to distinguish between Hermitian and self-adjoint operators.

Now, of course, if you already know what a self-adjoint operator is you might not care. Weinberg's two-volume 1995 book on QFT is actually much clearer on what they're good for. But suppose, like me, you wanted to understand, oh I don't know, say functional derivatives. Cahill is the only book that discusses them, but his definition is this:

A functional derivative is a functional

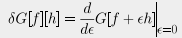
of a functional.

OK, fair enough, but what do they do, and why do we need them? Hassani has a page on them but doesn't say either, and Balakrishnan doesn't even mention them. Maybe no one knows what they do. Maybe they're not good for anything. But Penrose in The Road to Reality says we need them and you never, ever argue with Penrose.

Speaking of Penrose, none of these books has anything on spinors or twistors except Balakrishnan, who casually mentions spinors in his section on SO(3). Not under­stand­ing spinors will kill ya if you try to study particle physics.

A lot is made about those examples. I thought they would help to explain how the formulas are used, but while they do give you practice following math, mostly they just get in the way.  

Balakrishnan

The writing in Mathematical Physics: Applications and Problems by V. Balakrishnan is a model of clarity. I understood Fourier series pretty well until I read Cahill's description, so I turned to this book and found a beautiful, coherent explanation. The same is true for Laplacians. Instead of ten pages of formulas, you get an excellent, no-nonsense explanation of why the Dirichlet eigenvalues of a Laplacian relate to the frequencies of normal modes of vibration. That one sentence tells us why it's worth learning.

There are no irrelevant mathematical digressions, and the author even puts boxes around the most important formulas as we used to do in school. Balakrishnan covers many of the same topics as Cahill, including Green's functions, diffusion functions, Bessel functions, and the like, making them understandable without as much extraneous math, but unfortunately stops short before getting to the more advanced topics. I never thought I'd complain about a 778 page math book for being too short. This book is freely available online, but there's no errata list that I could find.

Another thing to know: these authors all seem to be able to factor cubic equations in their head. For those of us who can't do that, it might be a good time to get Matlab.

Hassani [no score yet]

At 1025 pages, Mathematical Physics: A Modern Introduction to Its Foundations by Sadri Hassani is the longest of the three, but it covers the fewest topics. There are big chapters on second-order linear differential equations, Green's functions, group theory, and Lie groups. By contrast, Balakrishnan has only three pages on Lie groups, which are essential for QFT, and Cahill has only half a page (and forgets to say why we need them).

Hassani's book is a bit more formal and rigorous than the other two and divides each topic into Definitions, Lemmas, Proofs, and examples. But after the first 500 pages or so, there are fewer Proofs and the text becomes more of an explanation in more formulas (and, occasionally, words).

There are many similar books out there, like Robert Geroch's 351-page Mathematical Physics (1985), which I haven't yet read but seems to cover a narrower range of topics with a big focus on vector spaces and topology. The back cover says it has an intuitive discussion of the “whys”, though I haven't verified it. Geroch has a theory similar to mine: “The greater the mathematical care used to formulate a concept, the less the physical insight to be gained from that formulation.”

It goes without saying that you need to review basic calculus and linear algebra before starting any of these books. They all assume you know things like integration by parts. But the best preparation is to start reading whatever physics book you want to study until you find yourself stuck. Then, grasshopper, your path will be clear and you will know what topics you need.

You can learn a lot from any of these books. You'll have to fight a lot harder to learn what the math means from Cahill, but the topics in Cahill are also a little more relevant to particle physics. Hassani is more traditional math style. But reading all three would be enough to make you want to forget about physics and go back to adding furin cleavage sites in viruses.

apr 13, 2024