Gauge Theories of the Strong, Weak, and Electro­magnetic Interactions, 2e

by Chris Quigg
Princeton, 2013, 482 pages
reviewed by T. Nelson

he weak force determines how nuclear particles decay. At high energies, it is unified with electromagnetism to create the electroweak force. As if by magic, electroweak theory also gives us the Higgs boson (H⁰), an uncharged particle that confers mass to leptons. It is one of the most successful theories in physics.

By now, every schoolchild who passed their first grade particle physics course knows the mass of the Higgs boson. Dads across the world are teaching their babies to say “125 GeV!” when asked “What is the mass of the Higgs boson?” But knowing its mass is one thing; knowing what it is, why it creates mass, and why we need it is another.

A boson is a force-carrying particle. Four of them, the W⁺, W⁻, Z⁰, and the photon, are involved in the electroweak theory.

Strengths

A unique feature of this book is that it explains the theory by first introducing theories that sound like they might work but are fatally flawed. This can be annoying if you're not prepared. For instance, in chapter 6 (“Electroweak Interactions of Leptons”) you go through several pages of complicated math, only for the author to tell you that it's all wrong because it predicts four massless gauge bosons when we know there is only one: the photon. So he starts over from scratch, deriving the Lagrangians a different way and gets to the correct theory, we hope, which predicts massive gauge bosons and a massless photon. That is what we want . . . almost . . . except it's still wrong: we had to assume that the electron had zero mass. So, back to the drawing board, and we finally end up adding a Higgs boson, which solves the problem.

This is deliberate. Quigg isn't reviewing the history; he's explaining why the new theories are necessary. Why do we believe in quarks instead of the older parton model, even though we've never seen a quark? There are people out there who don't believe in quarks, neutrinos, or mesons. There are even people who don't believe in wave-particle duality and think photons are particles moving up and down in a sine wave pattern. To understand why these things weren't just invented for fun, we must know why the earlier models don't work. Without the Higgs, for example, an electron would be massless. Electricity would travel at the speed of light. A lightning strike would blast away our atmosphere, and molecules would not hold together, which is bad.

Quarks

Quarks are explained by QCD (quantum chromodynamics). QCD is a non-Abelian gauge theory based on the SU(3) Lie group, which means there are 3 quarks and 8 gluons. A gauge theory simply means it is based on symmetries observed in nature. We know symmetries are important because Noether's theorem tells us a symmetry is equivalent to a conserved property.

There are three quarks in a proton and two in a meson. The current theory is that quarks are fundamental particles, like electrons and muons. In QCD, quarks have “color charge,” concept­ual­ized as red, green, blue, antired, antigreen, or antiblue. Only particles with no net color charge (e.g, rr_ or rgb) can exist.

Gluons have color charge like quarks, except that each gluon has two colors because its function is to hold two quarks of different color together. Unlike the older parton model, where the hadron is just a bag-o'-quarks, the newer model of perturbative QCD tells us that the quarks and gluons interact, and this is confirmed by experiments.

Gluons bind quarks together so tightly that, according to Quigg, if you tried to pull two quarks apart, the amount of energy you'd need would be so great that two new quarks would be pulled out from the vacuum (the same place where physicists seem to get some of those formulas), thereby creating two mesons instead of the original one. That's a roundabout way of saying it's easier for nature to make a new one than to tear an old one apart.

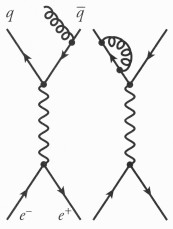
Feynman diagrams of e⁺e⁻→qq_ electron-positron annihilation showing radiated gluon (left) and virtual gluon (right) (redrawn from fig. 8.24, page 304)

Gluon radiation was a key piece of evidence for their existence. Radiated gluons aren't found in isolation, but in jets containing hadrons released after high-energy collisions. Gluons don't have mass, so they can't decay, but when a quark-antiquark pair containing a gluon is ejected from a nucleon, the gluon can radiate, creating a new shower of particles. Without gluons, there would be only two showers. Thus, the presence of 3 or 4 showers is proof that gluons exist. There are also, of course, virtual gluons (see figure).

The author includes experimental results that show the utility of the formulas. This is a great feature, as some other books tend to derive a large number of formulas and then stop, as if the sole point of physics is to invent formulas. But no matter how many pages it takes to write a formula down, it still needs to be confirmed and to be understandable by mortals in terms of the physics.

Unified theory

There are a great many things the current theory doesn't tell us. Many parameters, including hadron masses and flavor mixing, are unexplained. Indeed, there are 25 arbitrary parameters in the theory as it stands. It would also be nice to know why charge is quantized, why electrons and protons have the same charge (though with different signs), and how to cram gravity into the theory. It doesn't explain why the Higgs is 125 GeV and not somewhere above 1 TeV. And dark matter, dark energy, and the absence of antimatter are complete mysteries.

So the author ends with a (relatively) light chapter where he speculates about a unified theory called SU(5). This theory gives us, in addition to the 8 known gluons and the 4 electroweak bosons, 12 new scalar Higgs bosons, along with leptoquark bosons (X^±4/3 and Y^±1/3), which mediate conversions of quarks into leptons and vice-versa.

Those scalar particles are troublemakers, as they can mediate proton decay unless they are as massive as the gigantic leptoquarks (around 10¹⁵ GeV). Protons could decay into an e⁺ + π⁰ meson, into μ⁺ + π⁰, or some other pathway. The mesons produced could then be detected when they decay into gamma ray photons. By scaling up the rate of muon decay, you get a rough estimate of the rate: τ = 10³⁴ years. But a better calculation gives only 1.9 × 10³² years, which now rules out almost all versions of SU(5) because the Super-Kamio­kan­de detector proved that a proton survives at least 10³⁴ years. So SU(5) will need a lot of tweaking if it's going to survive.

To give you an idea how big a 10¹⁵ GeV leptoquark is, it would be about a quadrillion times more massive than a proton, or roughly 1.67 nanograms. One leptoquark would be 25 million times heavier than the DNA in the largest known virus (Megavirus chilensis, DNA = 1,181,404 base pairs).

It would also be nice to find an explanation for the famous vacuum energy density (Λ) discrepancy. The Higgs potential contributes a uniform vacuum energy density, but the predicted value is off by 54 orders of magnitude. SU(5) is off by even more: 10¹⁰⁰—a factor of a googol.

Weaknesses

The second edition was written after the Higgs boson (H⁰) was discovered at the LHC in 2012, yet long sections describing earlier speculation about its mass remain. Instead of re-writing this chapter, the author just stuck a couple new paragraphs here and there mentioning that the Higgs has been found. Again in the chapter on unified theories, he still says H⁰ mass is unknown. All these sections should have been completely rewritten (easy for me to say, I suppose) to tell us the implications of a 125 GeV Higgs and the long discussion about why it must be below 1 TeV and either 92+34−26 or 96+31−24 shortened.

The bits about proton decay are also out of date. Thus, this book is more like a modified first edition than a true second edition.

Many of the graphs are also found in other particle physics books, but this one is more mathematical and also explains in greater detail why the curlycues and dipsy-doodles in the current theory were necessary rather than just presenting it as a fait accompli as others do.

Prerequisites

While the theory is well covered, there's not much about the particle zoo or specific reactions of quarks. For instance, you won't learn which quarks are in the J/Ψ meson or its decay pathways, or why gluons have two colors. These physical details are essential to make the formulas seem meaningful. A good book on elementary particle physics, like The Quark Structure of Hadrons, is recommended.

You should also have some knowledge of QCD and quantum field theory (QFT). If you're just starting out, it's a good idea to pick a QFT text that covers what you want. QFT is a big topic; QFT books that just teach you how to calculate the invariant matrix elements (fancy M) from Feynman diagrams but not the Lie algebra or topics like spinors, tensors, and S-matrices aren't enough. Without this preparation, you could easily get lost. The best textbook is the two-volume one of Weinberg, who was instrumental in creating electroweak theory. A good review of Weinberg's theory, to appear in Nuclear Physics B, is here.

Another useful book is An Elementary Primer For Gauge Theory by K. Moriyasu, which explains the equations in understandable language. Weinberg uses Lie algebra, so an earlier book like Howard Georgi's 1999 Lie Algebras in Particle Physics (reviewed at right) may also be useful.

It's a lot of work, but the reward is enormous: it gives you a deep understanding of the universe and an appreciation of electroweak theory, and how it's not just a pile of formulas but one of the greatest achievements of our civilization. So, hurry up and learn it while we still have one.

feb 10, 2024

Lie Algebras in Particle Physics:
From Isospin to Unified Theories, 2e

by Howard Georgi
Westview Press, 1999, 320 pages
reviewed by T. Nelson

roup theory is the study of symmetry. Lie algebra is a convenient way of expressing symmetry, which became a big focus in physics when physicists discovered a fundamental connection in physical systems between symmetry and conser­va­tion laws. This is the celebrated Noether's theorem.

This book originated in a series of lectures by Nobel laureates John Van Vleck and Sheldon Glashow. Using a practical, informal style, it explains finite groups (including permutation groups / conjugacy classes), represen­ta­tions, characters, generators, Lie groups, and Lie algebra. The author uses a lot of Young tableaux, which are Tetris-like boxes that represent conjugacy classes: each box shape corresponds to an irreducible representation of a group.

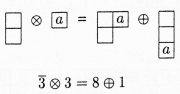Clebsch-Gordan decompo­si­tion of a group representation into its subgroups, drawn as Young tableaux (page 181).

These rep­re­sent­ations can also be ex­pres­sed as quantum states or, more conveniently, as tensors, and a lot of space in the book is used in showing how to use raising- and lowering operators to fill the states. The author also uses a sort of hopscotch notation to show how to construct quantum states. What you will learn is how to express these states in a variety of different ways, including Gell-Mann's famous symmetrical “eight-fold way” of grouping baryons in a hexagonal plot in Cartan space according to their quantum number (isospin I₃ vs hypercharge Y).

Each section in the book is a kind of puzzle, as none of the examples is fully explained, so the reader has to work out the missing details. For this, another text­book, such as Groups and Symmetries: From Finite Groups to Lie Groups by Yvette Kosmann-Schwarz­bach is occasionally useful. Kosmann-Schwarzbach gives a clear definition of the Clebsch-Gordan formula, which is a way of converting a tensor product to a sum of irreducible representations, for example, 3 ⊗ 3 = 6 ⊕ 3_. (These numbers don't always add up; they're a shorthand for mathematical constructs called Dynkin coefficients. For instance, (2,0) ≡ 6 and (0,1) ≡ 3_, where the 0, 1, and 2 are “representations” of quantum states and 3_ and 6 are the number of dimensions. The author says this is “not too confusing”. Kosmann-Schwarzbach actually describes it better, and gives a table.)

I also had to turn to Kosmann-Schwarzbach to realize that what Georgi calls ‘weights’ are actually particles. That book also provides a lot more history about the mathe­ma­tic­ians and their discoveries, but the text is more mathematical and abstract: mostly propositions and proofs and not as much physics.

Tensor operators might sound intimidating, but as Georgi says a tensor is nothing more than a wave­func­tion; the well known Levi-Civita symbols (ε_ijk and ε^ijk) are not really constants as most people think but invariant tensors that are widely used in defining permutations, especially in SU(3). (They aren't called Levi-Civita in the book; I suppose the reader is expected to know it). But if you don't like tensors, you'll love them after seeing the alternatives.

By Chapter 15, the book fully immerses you in particle physics, with discussions of isospin, the quark model, Higgs field, and spontaneous symmetry breaking, and then goes off into the weeds of SU(5), SU(6), and even SU(10), which despite their beauty aren't much discussed these days due to their predictions of proton decay, which doesn't seem to happen. There's also a chapter on Clifford algebras and spinors.

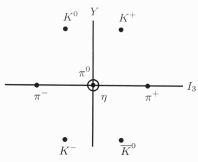Meson octet diagram (from Groups and Symmetries: From Finite Groups to Lie Groups, 2e, p. 152)

If nature were really sym­met­rical, all the particles in the famous octet of meson states would have the same mass, which they don't. In fact, most of the major discoveries, including the Higgs boson, which provides mass to leptons (such as electrons, muons, and tau) and quarks (although some dispute this latter point), seem to have happened because things are unsymmetrical, which is to say when symmetry is ‘broken’ with respect to the so-called vacuum state.

Of course, those symmetrical diagrams like the meson octet (shown above) aren't the same kind of symmetry that was originally meant. They're just an expression of the fact that their states are quantized. One could say that quantization and symmetry are a good match.

So, is symmetry really a part of nature, or is it just an intellectual construct that helps us fill in the missing pieces? Maybe principles like symmetry are essential for devising new theories, for understanding how things should work. But principles are also recipes for stasis. Just as in politics, you don't make any progress until you break them.

mar 05, 2024