a couple weeks ago physicists made a big discovery about socks: after you wash them,
you have to rinse them with water. If you rinse them with more detergent, some of the
detergent remains inside and they won't get clean. In all the times
people washed socks, nobody ever realized this before.
A sock and an anti-sock entangled
Physicists have learned much about the world by observing socks. Socks are made of string, so they can also tell us a lot about string theory and quantum entanglement.
Many people have noticed that whenever a sock disappears from your laundry, you always find a quarter. Of course, the price of a sock has gone up, but you still only get a quarter. That tells us about cosmic inflation.
People have long attributed this to sock fairies (indeed, there has to be more than one, by the same reasoning we use about Santa Claus). But there's a deeper truth about socks that many people don't know about: Only the left socks disappear.
I estimate that over the years I have lost 57 left socks but only 44 right socks. This could not happen by chance. But why do left socks decay faster then right ones? Does this reflect a fundamental asymmetry in the universe? Could it, perchance, explain why there is more matter than antimatter?
Physicists have often wondered why there is more matter than antimatter. They're finding many examples of asymmetry in the universe. For example, neutrinos are all left-handed, while anti-neutrinos are all right-handed. There's a deep connection there somewhere.
Perhaps, you might say, left and right socks are identical when they come from the factory, and parity (or handedness—or we should say footedness) is only imprinted on them when they're worn. In the dryer, left and right socks lose their parity but acquire charge, and they're converted into generic socks, just as the different flavors of neutrino (electron, muon, and tau) convert into other flavors. This is called neutrino oscillation. So if the phenomenon of sock oscillation exists, it might explain why some left socks still exist despite their shorter half-life.
But we also know from observation that when clothes dryers impart an electrical charge to socks, they attract each other. This means they have opposite charge, and so they are antiparticles. The dryer also gives them the same spin. This is why left and right socks don't annihilate each other.
Perhaps you might object, “But Dr Fippler,” you might enjoin, “Could it not be, sir,”—everyone is always terribly polite in my imaginary world—“that the reason you preferentially lose left socks is that your left foot is slightly bigger than your right, and therefore your left socks get stretched out more? And what about those of us who have the proverbial two left feet? In such cases, would not 100% of the socks we lose be left ones?”
To which I would reply that, indeed, physiological differences could preferentially introduce structural instabilities into one or another of a pair of socks. A person with inflammation in their left foot, for example, would eventually wear out all their left socks through thermal degradation.
But then you might continue, reaching further into social constructionism, “and aren't you discriminating against those who have no feet? People of footlessness have rights, too. Your theory is evidence of two-foot privilege, and you're being racist and doing violence to their dark gray footy bodies!”
A dark matter sock
To those people I would say: Go back and sit down. Also, I refer you to the classic physics paper On the Random Sampling of Pairs, With Pedestrian Examples by Arratia and Sesalvo, where the sock problem is modeled as a special case (only two colors) by a one-dimensional probability distribution. Their colorful three-dimensional graph shows the limit discrepancy D(p,q) where p = p(n,a/sqrt(n)) and q = p(n, b/sqrt(n)) where p and q are the probabilities of a match and mismatch, respectively.
Bertlmann's socks
Reinhold Bertlmann was a physicist who was famous for always wearing socks of two different colors. The idea was that if you know the color of one of Bertlmann's socks, you automatically know the other one will be a different color. It's the same with two entangled particles. We know from conservation principles that they must have opposite spins, so if we measure the spin of one we know the spin of the other, even if it's light years away.
Physicist Marian Kupczynski says quantum entanglement differs from the prediction of Bertlmann's socks:
Paradoxes are only found if incorrect models of sub-phenomena are used. . . . “An entangled pair of photons” resembled neither “a pair of Bertlmann's socks” . . . nor “a pair of fair and random dice.” . . . Any individual experimental outcome cannot be predetermined by a value of some variable assigned only to a physical system but it depends also on the variables describing the devices used in this particular experiment.
A famous paper by physicist John Bell titled Bertlmann's Socks and the Nature of Reality (J. Phys. Colloq. 42 (C2), March 1981) proved that socks do tell us a lot about quantum mechanics—namely that socks, unlike subatomic particles, have hidden variables.
Bell showed that the distribution of socks followed the Clauser-Holt-Horne-Shimony
inequality
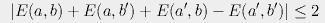
This, he says, does not happen in quantum mechanics, where we actually have
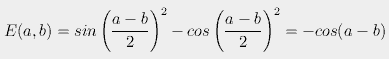
This tells us that if a hidden variable is local it conflicts with quantum mechanics, and if it agrees with quantum mechanics it cannot be local.
Okay, you might say, whatever. Getting back to the interesting stuff . . . we might predict that if the dryer rotates counterclockwise, left socks should preferentially disappear. If it rotates clockwise, right socks will preferentially disappear. This is equivalent to time going forward or backward.
Socks are an easy way for string theorists to study how strings work. Once that's done, they can work up to sheets, pillowcases, and towels.
Thus ends today's lesson on what socks tell us about charge-parity-time (CPT) symmetry, which is actually not as much as I originally thought.
apr 12 2018, 4:44 am. edited apr 15 2018, 4:04 am
