Springer Series in Light Scattering, v.6
Radiative transfer, light scattering, and remote sensing

by Alexander Kokhanovsky, ed.
Springer, 2021, 196 pages
reviewed by T. Nelson

here's no better way to start the winter season than by reading a book by a bunch of Russian scientists writing about the three things Russians are experts at: snow, ice, and radiation.

This book, volume six out of nine so far, contains three big articles: one on the √ε law, one on solar heating of snow, and one of stereological methods to study ice particles.

Radiation and the √ε law

In the first chapter, V.V. Ivanov is enthusiastic about the √ε law. Unless it escapes into space, the inevitable fate of a photon depends on ε (in this context, ε means extinc­tion coefficient, i.e. the probability of destruction of a photon, not permittivity) and β (the absorption coeffic­ient). Whichever term is bigger tells us whether a photon gets scattered or absorbed. Ivanov traces the history of formulas used in solar astrophysics that use the √ε law to calculate S_h(τ).

What is all this S_h(τ)? τ is the thickness of a layer in the atmosphere where escape of radiation causes deviations from local thermodynamic equilibrium. S_h(τ) is called the vector source function in a famous formula known as the homogeneous Wiener-Hopf equation, which tells you the ratio of emission to absorption. When ε is close to zero, there is more re-radiation (i.e., scattering) than collision.

To fully understand this chapter, the reader would need some background knowledge of radiative transfer, for which there is only one good textbook that I know about: Radiative Transfer in the Atmosphere and Ocean by Thomas and Stamnes. That book is good for most topics, though its discussion of scattering could be better organized. Some knowledge of solar astrophysics also wouldn't hurt.

Another book, Radiative Transfer: An Introduction to Exact and Asymptotic Methods by Hélène Frisch, is good for understanding the math, of which there seems to be a great deal, but doesn't make much effort to relate the math to any physics. Once the reader gets to the end of Part I and understands all the Hilbert transforms, Cauchy integrals and whatnot, Frisch just moves on to polarized radiation, which is totally different. My advice would be to first read Bohren and Clothiaux's book (reviewed at right) to understand why it's interesting, then come back to this one. That's how science works: you have to gain an interest in the topic first, then trade the interest to gain knowledge. When we know everything about a topic, we come out even. I suppose life works that way as well.

Back to Ivanov. The most interesting part of Ivanov's chapter is about anomalous diffusion. Anomalous diffusion (not to be confused with anomalous diffraction) means that photons don't follow a random walk like particles undergoing Brownian motion. Instead they follow a Lévy flight, where they make many short distance hops followed by big hops that are 10,000× longer. This is caused by CFR, or complete frequency redistribution. When a photon is absorbed, it “forgets” its original wavelength. When it is re-emitted during scattering, its wavelength can be anywhere within the spectral line. If it's near the center of the line, it gets absorbed quickly by some nearby gas molecule. If it happens to be at the edge, it travels a long distance before it gets absorbed again.

Snow

A lady from Hong Kong once told me she had never seen snow in her life. That's a darn shame because, as this chapter shows us, snow is very interesting. In a snowbank, near-infrared radiation is absorbed at the surface and visible light from the Sun is absorbed deeper in the snow. Infrared emission occurs only from the surface because snow and ice are opaque in mid-IR.

Emitting IR makes you colder, which is why most solar melting occurs deep under the surface. The inside of a snowpack can be as much as ten degrees C warmer than the surface. That's why phytoplankton and gas bubbles are found there, and why it melts before the surface. The author says radiative cooling in the mid-IR (8–13 μm) from the surface is limited at night but stronger in the daytime.

The complex index of refraction (m) of ice is given by the formula m(λ) = n(λ) − iκ(λ), where n is the index of refraction and κ is the index of absorption. This important formula, which comes from the Kramers-Kronig relation, tells us that RI is a complex number, a sum of real and imaginary components that vary according to wavelength. If the imaginary term is bigger, the object acts as a metal. If the real part is bigger, the object acts as a dielectric and transmits and refracts light. In the case of ice, n decreases from 1.4 to 1.1 and κ increases dramatically as λ goes from 0.4 to 2.8 μm. This tells us that the optical properties of ice and snow are dramatically different in the infrared compared to visible light.

Even small amounts of soot cause more heating in deep layers. Soot, like air bubbles, induces thermal stresses, which cause cracking. Gas bubbles cause scattering and absorption between 0.6 and 0.7 μm, reducing the penetration depth and increasing conductive heating in deeper layers. According to the authors, air bubbles change the color of ice from violet to blue, but don't explain why icebergs are green.

Ice

The third chapter discusses stereology, which is the part of probability theory that deals with geometrical statistics. That makes it useful for studying how light passes through 2-phase conglomerates of ice crystals in a medium that has a different RI. The idea is to define ξ as the chord length, which is the length of a light ray between one end of an ice crystal to another. With some assump­tions, the distrib­ution function f(ξ) can tell us a lot about the particles. For instance, if f(0) ≠ 0, the phase has sharp edges. If f(ξ) ≠ 0, there are connected regions in the phase at scale ξ.

This is obviously good to know, and the author goes through some intimidating math using Fraunhoffer diffraction, Rayleigh-Gans, Wentzel-Kramers-Brillouin, and geometric optics to calculate chord length distrib­ution of irregular particles. For instance, they calculate that photon survival probability ω₀ in ice is minimal at 1.45 μm, making it black at that wavelength. Aged white ice with ξ = 3 mm absorbs the most, with an ω₀ around 10%.

Even in the visible, they say that Arctic and Antarctic ice and snow also sometimes absorb blue light, turning it yellow. They blame this on dissolved organic matter and say it's from seawater. Yes, seawater, not the other thing, but you still shouldn't eat it.

oct 24, 2023. updated nov 03, 2023

Radiative Transfer

by S. Chandrasekhar
Dover, 1960, 393 pages
reviewed by T. Nelson

his book on the mathematical theory of radiative transfer, oriented toward stellar astrophysics and neutron scattering, is often cited in other texts.

The book is almost solid math, but there's no cowboy math here and no skipped steps as you find in more modern texts. The author first presents the theory using formulas that are totally unsolvable, and only later describes the real formulas that people actually use. This makes it possible to figure out where he's going at each step. It also gives you an under­stand­ing of why those particular formulas are used and not others. For example, his explanation of Legendre poly­nom­ials and what they're good for is beautiful in its clarity and simplicity.

Two disadvantages of this 60-year-old book is that it's mostly about scattering, and there are many more formulas than anyone really needs. There's little guidance as to which of them are actually usable or whether they are confirmed by measurement. Absorption and similar topics related to anything physical aren't covered well. Climate, nuclear reactions, and chemical reactions are not covered at all. There are no exercises, no experimental data, no pictures, and no practical applications. Just math.

Even the author admits that some of the formulas are so complicated that they give no insight into the physical processes. But that doesn't stop him. For instance, he manages to make the Law of Darkening, which we now call limb darkening, sound inscrutably complicated when it's actually not. For some reason I just got a terrible headache after reading all this.

nov 10, 2023

Fundamentals of Atmospheric Radiation: An Introduction With 400 Problems

by Craig F. Bohren and Eugene E. Clothiaux
Wiley-VCH, 2006, 472 pages
reviewed by T. Nelson

his book starts with the same material as Chandrasekhar's book (reviewed below): E = hν − p, then works up to the two-stream model, where some photons propagate up in a ‘slab’ of the atmosphere and other photons propagate down. From there, we get multiple scattering, then a more advanced treatment of multiple scattering, followed by polarization. The difference, and the strong point of this book, is that it also teaches the reader how to think like a physicist.

By page 17, Chandrasekhar is up to multi-line equations like this one for Rayleigh's phase function:

p(μ,φ;μ′,φ′) = ¾ [ 1 + μ²μ′² + (1−μ²)(1−μ′²) cos² (φ−φ′) + 2μμ′(1−μ²)^½ (1−μ′²)^½ cos(φ−φ′)]

while Bohren and Clothiaux are telling us stories about a colleague who tried to explain the photoelectric effect without photons. This task, akin to explaining gravity without mass, required immensely complicated math. At one point, according to the authors, the speaker acci­dent­ally used the word ‘photon’, at which point the author jumped up and shouted, “Photons! You promised no photons!” Or so he says.

So, while other books give you formulas, this one gives you not only the formulas but a solid understanding of what the formulas actually do, and more importantly what they don't do, and why we should be skeptical of them. They say “[A]ll theories are ultimately wrong. And a theory is just scribbles on paper, not reality.”

That's important, because radiative transfer—emission, absorption, and scattering—in a clear sky is described well enough by the formulas, but clouds are another matter. It's surprisingly hard to torture the formulas into telling us the truth about clouds. All we know for sure is that they consist of water droplets around 10 μm in diameter. (Bigger droplets, say 40 μm, exist, but they're a million times less abundant. The big ones are responsible for most of the radar backscatter.) And though they appear white to the eye, in infrared they're black—almost as black in IR as snow, which the authors say is the blackest natural material on Earth at wavelengths above 1.4 μm.

Gases absorb radiation in sharp lines, not in big smooth bands as we're taught in school. As the authors' spectrum of air containing water vapor (below) shows, there is also a lot of overlap: 15 μm is often cited as the main peak for CO₂, but water absorbs there as well.

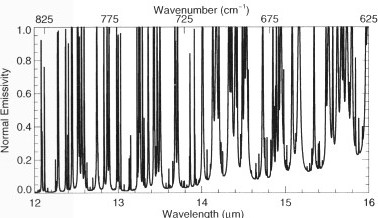
Contribution of water vapor to infrared emissivity of air. According to Kirchhoff's law, emissivity is equal to absorptivity. (Source: Fundamentals of Atmospheric Radiation, p.28)

That is something students really need to know. Memoriz­ing formulas isn't enough; you also need the physical insight to tell you whether the formula is making sense.

The authors are also very skeptical about models. Here is the most important sentence in the book:

[A]ny calculations of absorption at wavenumbers sufficiently small to resolve all absorption peaks and troughs over solar and terrestrial spectra would require computing time not measured in seconds, minutes, or even hours but days, weeks, months, years, possibly lifetimes. [p.329]

The fact that thermal photons from the surface are absorbed as narrow bands makes them highly susceptible to saturation. The authors plot the absorptivity of CO₂ at 758–746 cm⁻¹, a minor absorbance band for the gas, and note that saturation is clearly occurring even at 180 ppm (p. 107).

How to model a cloud? Clouds are scatterers, but Mie scattering formulas are way too time-consuming to calculate. Modeling a rainbow needs 10,000 terms, and it's still not good enough because raindrops aren't spheres, as required by the theory. So what's often done, say the authors, is to use the Henyey-Greenstein phase function. Unfortunately, this formula only works for some types of clouds, and it's off by a factor of 100 at some angles, such as for forward-scattered photons, so it's necessary to throw in fudge factors . . . er, corrections . . . for the scattering coefficient and albedo. Clouds are modeled as rectangular boxes; assumptions and approximations like this are needed in almost every equation. The math, as invented by the Old Ones like Rayleigh, Mie, and Chandrasekhar, works but only within certain limits. Sadly, many of those formulas are unsolvable because they refer to things that can't be measured, so approximations are the norm for this branch of science.

The unstated question is: how well can models that make so many approximations capture what is really going on?

The authors also give us useful aphorisms: “Repetition [of some scientific claim] increases the probability of incor­rect­ness”.“Nothing of great moment has been discovered in the shower”, and Stigler's law of eponymy (no scientific discovery is named after its original discoverer).

You'll also learn lots of facts that will make you very popular at Christmas parties, like the fact that snow is blue because of absorp­tion of red light, not scattering as many people think. Wet sand is dark because the refractive index of water is close to sand, so more scattering is peaked in the forward direction, making it dark. The sun was blue in 1950 due to oily smoke. And radiometry, they say, is actually an acronym meaning Revulsive Archaic Diabolical Invidious Odious Mystifying Exotic Technology Regenerating Yawns.

That's how real scientists talk. They're iconoclastic and they know a lot of stuff that normal people don't. It takes great skill to make this a subject like radiative physics enter­tain­ing. It can only be done by people who love the subject and are having fun at their job. It makes this book entertaining to read (within certain rigidly defined parameters, of course; it is, after all, a physics textbook).

I was so sad in my brief return to academia to discover that that spirit of enjoyment is now almost gone. No one tells jokes to a class anymore. The students would report you. Someone would get triggered.

As for those 400 problems, some are calculations, but most are essay questions that test your conceptual under­stand­ing. That is what the authors consider most important, and this book provides it. As the authors say: the good mathema­tic­ians know in their bellies what is true. Proofs are just for convincing others, and crunching numbers is for dorks (though they don't call them that, exactly).

Of course, there are some oversimplifications. Essential topics like CFR (complete frequency redistribution) and Lévy flight aren't discussed. White paper doesn't really produce speckle from a laser (or at least, I've never been able to get it). Paper contains fibers with varying amounts of fluorescent dye, which is why you can't use it for flatfield corrections.

Like most real scientists, they're noncommittal about the global warming hypothesis. Politics are for others; these two just love looking at clouds. They rant more about how Kirchhoff and Snel's names are routinely misspelled than anything else. That makes this book the most interesting, credible, and entertaining physics textbook I've ever seen.

And I have to admit, thinking of clouds as large black boxes is a great idea.

dec 11, 2023. updated dec 12, 2023. figure added dec 13, 2023

Correction: An earlier version of this article said that radiometry is Revulsive Archaic Diabolical Invidious Exotic Technology Regenerating Yawns. This has been corrected to Revulsive Archaic Diabolical Invidious Odious Mystifying Exotic Technology Regenerating Yawns.