Quantum Measurement: Theory and Practice

by Andrew N. Jordan and Irfan A. Siddiqi
Cambridge, 2024, 264 pages
reviewed by T. Nelson

eople sometimes think quantum phenomena are mysterious, counterintuitive, and indeterminate. The problem, according to the authors, is that such interpretations are “too often an ex post facto forcing of physical phenomena into contorted mental constructs” which create contradictory ‘interpretations’ that end up as topics of philosophical debate.

Take the idea that measuring an entangled quantum state destroys it by “collapsing the wavefunction,” which is to say it produces an instantaneous and irreversible transition from an indeterminate quantum state to a classical definite state. This is the ‘decoherence’ idea that was supposed to solve the measure­ment problem, but instead gave rise to speculation about what constituted ‘measurement’, as in the embarrassing situation of that poor cat.

Recent work on qubits has shown that, contrary to what we're told, quantum measurements take time, they are reversible, and quantum systems can be controlled and measured without destroying them. Including the measurement apparatus in the formulas is essential for the theory to make sense. Ignoring measurement, say the authors, is holding back quantum physics.

What is a qubit, anyway? The authors describe transmon qubits, which are electronic circuits containing two (or more) superconducting Josephson junctions encased in a heavy aluminum box which acts as a resonant cavity. The Josephson junction is a nonlinear oscillator that has two states: a ground state |g⟩ and an excited state |e⟩, often written as |+⟩ and |−⟩ states.

Transmon qubit circuit from Fink et al.^[1]. The ⌧ symbols are qubits. The authors say they are 5 μm across and held in a reson­at­or at a temperature of 20 mK

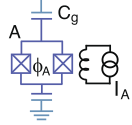
In a transmon qubit, which they describe in detail, a phase-sensitive amplifier creates a squeezed state by amplifying one half of the I-Q quadrature and squeezing the other, so the total noise is preserved. A pulsed microwave signal drives transitions between quantum levels, creating a quantum superposition. For reasons far too complicated for a book review, the |e⟩ state is the only state that can decay, which it must do by quantum tunneling. If it decays, you get a tiny change in the frequency of a signal via a phenom­enon known as the Stark effect that can be measured by a superconducting parametric amplifier, which is one of the most remarkably sensitive current measuring devices known—capable of measuring a single microwave-frequency photon. If there's no signal, you assume it's in the ground state. By using squeezed states, it's possible to reduce the noise below the standard quantum limit.

There are also optical qubits that use quantum dots to produce photons that can be selected in a special (and expensive) high precision optical filter known as Fabry-Pérot cavity and measured in a Mach-Zehnder or Sagnac interferometer. Optical qubits follow the same equations as phase qubits, but measure the index of refraction instead of using the magnetic Hall effect. These are described in Bachor and Ralph's A Guide to Experiments in Quantum Optics 3e.

The challenge is how to measure the state of a single photon, which is in a superposed state, without destroying it. That is, how to get information from it without destroying its coherence. The general idea, as described by the authors, is captured by the concept of a weak measurement. In a weak measurement, you extract only tiny hints about the state at a time, which means you have to do many weak measurements to get one bit. This way you can measure a quantum state without disrupting it and causing it to lose its superposed state. It also means the measurement can be reversed by putting the information back into the qubit.

This tells us something profound: wavefunction collapse is not instantaneous. It can be measured, controlled, and un-collapsed. All this has been empirically demonstrated. There are, of course, still challenges in doing error correction in qubits and making them last longer. But who would ever have guessed that the key to solving the measure­ment problem would be to actually do measure­ments instead of just theorizing? The authors give a general principle:

If the observable being measured does not commute with the system Hamiltonian, then there is in general an exchange of energy between the system and the measuring apparatus.

In English, that means if you repeatedly measure, eventually you're not getting accurate measurements because it draws energy out of the system.

In the eleventh chapter of this book, the authors tell us what all this means for the supposed mystery of quantum phenomena:

If anyone tells you 'science' says this or that, they are a liar. A quantum state is not a state external to us—it is a state internal to us.

The authors say that wavefunction collapse is always correlated to the amount of information you can get, but a wavefunction can be un-collapsed if the information is contradicted by another measurement. They sum it up by describing what they call the ‘epistemic view’:

The likely best answer to what the meaning of a wavefunction is, is that it does not exist—only measurement outcomes do.

This book is a little technical and some background in quantum mechanics and microwave electronics would help, but it's a ground-breaking book and short enough to be read two or three times. In fact, just the fact that there's a quantum mechanics book that's only 264 pages long is pretty ground-breaking by itself.

[1] Fink JM et al (2018). Dressed Collective Qubit States and the Tavis-Cummings Model in Circuit QED. arXiv:0812.2651v2

oct 02, 2024

Optics Measurements and Demonstrations for Student Laboratories

by Stephen Lipson
IOP, 2020, 203 pages
reviewed by T. Nelson

his is half textbook and half idea book for optics instructors. It starts out with basic information about how to clean surface-coated mirrors, how to use an autocollimator to measure the focal length of a lens accurately, and the science of polarization. It then gradually works up to more sophisticated experiments including interferometers, ptychographic microscopy (where you take images of objects smaller than the wavelength of light), evanescent wave optics, acousto-optical effect, non-linear optics, and quantum optics.

There are lots of details that ordinary textbooks won't tell you, like the fact that corn syrup is birefringent (meaning you can observe interesting colors under crossed polarizers), you don't need lithium niobate to observe an acousto-optical effect, how to make a model of a gravitational lens, how a quarter-wave plate works, how to make a hologram, and which interferometer design is appropriate for someone on a small budget. The chapter on materials tells you that gelatine and PMMA (polymethyl methacrylate) become birefringent when stressed. (Upon checking that fact for this review, it also turns out that gelatine, celluloid, and paraffin also happen to be phosphorescent at cold temperatures.)

This is not a lab manual: some of the experiments involve using up to 1000 volts and high power lasers. There are no safety warnings or step-by-step procedures, just ideas for interesting and colorful things you could learn in a lab course. Access to the scientific literature and other reference material would be needed to get the details. There's very little optics theory, only a little math, and—get this—no Maxwell's equations; the author recommends Born and Wolf if you want all that.

If you're a student, give this book to your instructors and demand that they teach this stuff to you, using protest signs if necessary. Maybe even chant slogans—“What do we want? Quarter wave plates! When do we want them? Now!” Probably give them a heart attack.

Lots of diagrams of the various setups and color images but no index.

oct 02 2024

A Guide to Experiments in Quantum Optics 3e

by Hans-A. Bachor and Timothy C. Ralph
Wiley VCH, 2019, 565 pages
reviewed by T. Nelson

his book is mainly concerned with optics, not just qubits, where microwave technology has mostly taken over. The first six chapters are reasonably good descriptions of basic topics like beamsplitters, interferometers, cavities, and lasers. Then, starting on page 232, the authors get to their real interests: single photon generators, quantum noise, and squeezed light.

A unique feature is the detailed descriptions of recent experiments in quantum optics. There's also some useful information, like a table of photon sources and their g⁽²⁾ values, where g⁽²⁾ is the probability of having more than one photon in each of the outputs. They include an electronic circuit diagram of an amplifier for a non-quantum-limited photodetector and, of course, many diagrams and illustrations of optical bench setups, which get fairly complicated. The authors say a common trick to cut noise is to use a heralded noiseless linear amplifier (NLA) in which a photon detection in one branch determines or “heralds” whether a detection in the other branch is to be counted or not. This is a roundabout way of saying they use a coincidence detector to measure only two-photon events.

One weakness of this book is that too much space is spent on simple topics. It's also a lot more verbose than it needs to be. For instance, they take eight pages to describe a spectrum analyzer. And there are a few big calculation errors here and there. It's also older, so with all this in mind you might want to wait for the next edition.

The authors' main interest is squeezed light, which allows you to measure phase or amplitude more precisely by moving the ‘fluctuations’—there'd be no quantum mechanics without fluctuations—between the two quadratures. You can make squeezed states with a non-linear medium or an optical parametric amplifier to reduce phase noise. The authors make the concept more understandable by describing it semi-classically as a way of reducing the sidebands of the quantum noise. In coherent light, they say, quantum noise is made of frequency-independent beat signals from the sidebands of the complex amplitude. They're added in quadrature and are uncorrelated, i.e. white noise. In a squeezed state, the sidebands are correlated with each other. So, in effect you're increasing the amplitude modulation and reducing phase modulation.

A detuned cavity can rotate the quadratures by adding a phase shift. But unfortunately, passing squeezed light through passive optical components reduces the amount of squeezing. And, the authors say, a squeezed state is more likely to have an even number of photons than an odd number because photon pairs predominate in the squeezed state.

The authors then talk about the interferometer used in the LIGO gravitational wave detector and how squeezed light would improve its sensitivity. Indeed, squeezed light was incorporated into LIGO shortly after this book was published.

There's also something called a quantum laser pointer, which sounds like something nice to have at a seminar. It increases directional pointing precision by a factor of two. It's also useful for optical tweezers. (Unfort­unate­ly, it's way too big to carry around.)

In the chapter on quantum key distribution, the authors say the sender (Alice) prepares photons entangled with vertical and horizontal polarization in a predetermined (“random”) sequence and sends one to Bob and keeps the other. This is clearly not unconditionally secure; the security relies on the algorithm used to set the polarization. It's security by obscurity. But if Eve doesn't have the key in advance, she's ficked. Eve can't just record the message and decrypt it later; she must have cracked their cipher well in advance, otherwise she'll turn the message into noise. The idea is that Eve will give up and go the tanning salon, where she can get all the photons she wants—and nice, high-energy UV ones, too.

The problem with using polarization, say the authors, is that optical fibers are birefringent, so polarization encoding gets scrambled. They suggest using interfer­om­eters instead. And using the standard 1550 nm (infrared) window in telecom fibers is no good either, because it requires special GaAs photodetectors to detect the individual photons.

Then there's the problem of quantum non-demolition, where you can measure a photon state and maintain it at the same time. This is not supposed to be possible, due to back-action, but the authors say it can be done using non-linear processes to transfer all the back-action noise to the quadrature that's not interrogated. So Eve's task is getting easier. Plus she's now tanned and rested. Maybe, Eve's probably thinking, if Bob knew about all those secret messages Alice has been sending to Frank, George, and Harry, he'd dump that shameless hussy.

oct 09 2024