Modern Cryptography With Proof Techniques and Implementations

by SO Hwang, I Kim, and WK Lee
CRC Press, 2021, 484 pages
reviewed by T. Nelson

t first glance this book looks rigorous and mathematical. The goal of the three Korean and Malaysian authors is to show that it's possible to prove stringently whether a cryptography system is secure. The idea is based on Shoup's Modular Proof, which says:

If (smaller protocols are secure and) some problem X is computationally hard, then the main protocol is secure.

Of course the authors know this isn't neces­sarily true, but it's a viable starting point to teach students. The goal is to derive and prove equations like this one purporting to show that a scheme is secure:

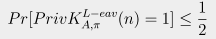
This formula means that the probability (Pr) of all that stuff in brackets is one half, the idea being that if an attacker guesses one bit and has only a fifty-fifty chance of being right, the probability of guessing it is “neglig­ible,” which means it is secure. The drawback is that we need an actual number here. Getting to this point depends on knowing what the attacker does. So, for example, they might say that the probability of guessing the answer is q_D/q, where q is some large number. This is nice and quantitative, provided of course that the attacker is nice enough to use a standard method like brute force.

Think of it as a newspaper. If everything they say is a lie, you still get the news by assuming the opposite of whatever they say is the truth. But if 50% of the stories are true and 50% are false, you get no information at all. The news is in an unbreakable code and only the reporter knows what's really true.

Needless to say, not knowing what an adversary will do is what makes devising a secure cipher such a challenge. I'm no expert, but it seems to me that an information-theoretic approach, with concepts like diffusion and entropy, along with a dash of complexity theory, might also be needed. For example, a good S-box (a key component in block ciphers such as DES and AES) has to fulfill specific criteria about non­lin­ear­ity, algebraic degree, and differ­ential uniformity. How to fit all that into those reduc­tionistic formulas doesn't sound easy.

The chapter on lattice codes was so dense as to be nearly incomprehensible, but the writing in the other chapters is clear and understandable but makes prolific use of acronyms, giving us paragraphs like this on page 51:

To achieve security, block ciphers are run in certain modes of operations including ECB, CBC, and CTR mode. It concludes that the ECB mode is not IND-CPA secure while CBC and CTR are IND-CPA secure.

The book really needs an list of acronyms. If you don't write them down as you go along, you'll soon be SOL.

While there's some discussion of RSA and D-H, as well as elliptic curves and group theory in the section on fundamentals, most of the discussion is on IBE, or identity-based encryption, which is similar to public key encryption except that information about a client is used. One example is broadcast encryption, where you pay a company not to encrypt their message. (Technically they still encrypt it, but give paying customers a key.) This is sort of the reverse of normal encryption in that it motivates clients to give away their private keys, so a content tracing scheme is needed to prevent it. The authors also talk about the encryption in bitcoin, pointing out that modern ASICs are 100 to 100,000 times more energy efficient than using a GPU, which has gone out of favor.

As for the ‘implementations’ alluded to in the title, the authors made the source code available on Github.

This book started to get almost exciting for a while, where Alice and Bob, perhaps having gotten tired of sending each other secret messages, start ‘concaten­ating’ each other—a sexual innuendo if I ever heard one. Alas, the budding romance was short-lived, and in general you'll need several cups of coffee and maybe something crunchy to keep you awake while reading it. So I give it four stars, three cups, and one bag of pretzels.

aug 28, 2023

An Introduction to Modern Cryptography, 3e

by Jonathan Katz and Yehuda Lindell
CRC Press, 2021, 626 pages
reviewed by T. Nelson

he goal of this one is to show that “modern” cryptography, unlike the classical kind, uses rigorous proofs of security and formal definitions that have transformed the field from an art to a science.

If Bruce Schneier's book was called Practical Cryptography, this one might be called Impractical Cryptography. It turns out that no one is sure whether most of the basic cryptographic primitives possess the attributes assigned, as people like to say these days, at birth. For instance, there's no way to prove that factoring a big number is actually hard. In fact, no one can prove that a one-way function is even possible. So, much of the foundation of modern cryptography rests on conjectures that are hoped or at least assumed to be true, at least as far as anyone outside the government knows. In other words, if the building blocks are secure, and if they're implemented correctly, and if combining the blocks together doesn't compromise something, then the scheme is secure. That's true, of course, but it's also a proof of Wittgensteins's claim that all true deductions are tautologies.

For example, on page 150 they write:

[I]f a scheme has indistinguishable encryptions under a chosen-ciphertext attack then it has indisting­uish­able multiple encryptions under a chosen-cipher attack, defined appropriately. [emphasis in the original]

Again, this is true given that 'appropriate' means, by definition, those conditions under which the claim is true. In short, many of the proofs are more aspirational than dispositional.

The book is in three sections: Classical Crypto­graphy, Private Key (Symmetric) crypto­graphy, and Public Key (Asymmetric) Crypto­graphy.

In Chapter 7 of Part 2, the authors describe how specific stream and block ciphers, including Trivium, RC4, Chacha20, AES, and DES, are constructed and how some of them can be broken. The authors warn the reader not to try to implement them until they learn more, not to try to create a new cryptographic primitive, and not to use just any old elliptic curve but to get one from NIST. However, from a learning point of view, ignoring that advice might make it easier to understand why the attacks work. In fact I'd buy a book devoted to these topics if there was one. Maybe they could title it Things That Can Go Wrong If You're Crazy Enough To Invent a New Crypto­system, Volume I.

However, they do provide worked concrete examples on some topics, including group generators, differential cryptanalysis, and elliptic curves. The detailed concrete example on differential cryptanalysis, a concept that is mostly covered by hand-waving in other books, is particularly welcome.

Another advantage of this edition is the improved coverage of stream ciphers, which have experienced a revival after the WEP debacle thanks to more secure algorithms. They are generally smaller and faster than block ciphers.

Building a toy primitive on your own is probably necessary to get any real benefit of this book. For example, for some of the sample calculations on the Chinese Remainder Theorem the answer is equal to the starting number, making it tricky to know if you did it correctly. Some parts of the text are clear, while the meaning of terms like “input-output pair,” while obvious to someone who has tried to break something, might not be apparent to an inexperienced reader.

That said, this book is a lot easier to read than Antoine Joux's book, but it's not for beginners. Each section has three parts: the proofs, the specific systems, and the math. The authors assume some familiarity with the encryption primitives like S-boxes and shift registers, and the math is mostly group theory and number theory, so it couldn't hurt to read a more introductory book to avoid getting bogged down.

The biggest weakness is the lack of implementation details: the algorithms are not really algorithms, but unimplementable high-level overviews. In the description of Feistel networks, for example, they say a math function is needed to make it actually work, but don't say what it is. (Maybe it can be anything?) Indeed, none of the sections on permutations (which they call bijections) provides enough detail to fully understand where the bits are going, how to calculate the amount of diffusion, or how to get all those little bits and pieces back together.

As with every other book on this subject, about three-fourths of the way through I got a strong impression that I should have read Oded Goldreich's Foundations of Cryptography instead. Just as in the old days when they always ended up telling you to read William F. Fried­man, there are some things you can't keep secret forever.

Interesting tidbit: Leslie Lamport, the person who wrote a definitive book on LaTeX, is mentioned in the chapter “Post-Quantum Cryptography” as the inventor of a cryptographic one-time signature scheme.

sep 12, 2023