
|
book reviews
Statistics booksreviewed by T. Nelson |

|
book reviews
Statistics booksreviewed by T. Nelson |
Most statistics books fall into one of three classes: introductions that explain things most researchers already know, books on mathematical statistics that derive things almost nobody cares about, and books on how to use some software for which the reader has lost the manual[1]. I know of no book that satisfactorily addresses the questions below, which I've had to argue over with people:
The answer to the second part of #1 seems to be ‘never’, and the answer to #2 seems to be that it depends on what hypothesis you are testing. Yet most papers never state their hypothesis. This may be the source of J.P. Ioannidis's conclusion that most published research findings are false (this conclusion is, however, based on flawed reasoning).[2]
The answer to #3 is still a mystery and may be better left to a book on what used to be called abnormal psychology.
I've concluded that the only sure way to understand statistics is to program the equations into a computer yourself and play with them. That's how I found out why a t test always predicts half the number of subjects as a power analysis with β=0.8. None of these books below explain that odd fact.
No matter how good your software, your statistics will only be as good as the language you use to describe them. Subtle changes in wording can make a big difference. For example, in Biostatistics for Medical and Biomedical Practitioners (reviewed below) the author calculates these two results:
This demonstrates just how important it is to be precise about the question you're asking, the test you're using, and the precise population you're referring to when quoting a statistic.[3]
[1] This is a polite way of saying they ‘borrowed’ their copy of the software from a friend.
[2] Ioannidis's argument was that there are a vast number of possible hypotheses but a finite number of true ones. The ratio of true to false ones may be, say 10/100,000 = 10−4, which is much less than the standard p<0.05 used for accepting a finding as probably true.
I can't tell whether he was serious or only being facetious, but it's easy to refute. Each discovery contributes one bit of information to our total store. For example, the question of whether eating bacon causes heart disease can be answered with a yes or a no, so its information value is one bit. Therefore, one could just as well argue that at least half of all scientific discoveries are automatically guaranteed to be true!
[3] The author gets the calculations right but states it wrong in the book.
Reviewed by T. Nelson
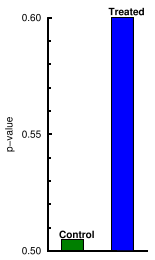
There's something about medical school that is devastating to people's math skills. The bar graph below, from somebody's research grant, is a perfect example. The PI, faced with the task of fluffing up a meaningless result, plotted two statistics in a bar graph and then started the y-axis at an arbitrary point just below the lowest number to make it look like a big change. But in fact it is a depiction of nothing.
The author says this book was written for physicians who need to brush up on their statistics. This is one of the few books in which most of the statistical tests that physicians and biologists need to know, like power analysis, ANOVA, Bonferroni correction, and odds ratios, are well represented. It uses a narrative style like the popular Statistical Methods by Snedecor and Cochran. Statistics are illustrated by interesting medical facts and paradoxes that turn up when diseases are analyzed statistically, and the writing style is excellent. It also has interesting historical facts, like the fact that Florence Nightingale invented one form of the pie chart and that it was not Mendel, but his gardener, who tweaked his plants to make his statistics come out right.
A good example of how statistics are often misreported was the 1999 report that claimed that blacks and women were 40% less likely than whites and men to be referred for cardiac catheterization. This was widely publicized in the press, and cited as prima facie evidence of discrimination. But when examined by a statistician, it turned out to be just an artifact caused by the original author not understanding the difference between odds ratio and risk ratio. The actual rates of referral were practically identical.
Hoffman, who does statistical reviews for journals published by the AHA, repeatedly advises doctors never to try to calculate anything by hand, even with a calculator. To make sure these doctors don't try to do math, no statistical tables are provided. Instead, readers are directed to various online calculators. My experience working with doctors suggests that this is very good advice.
Each chapter has references to the original literature. The writing is usually clear, but sometimes not. A physician will probably find the discussion on error propagation, which is a very important topic, to be thoroughly opaque. Mathematical topics, like differential equations, which are necessary for error prop, and beta and gamma functions, which are needed for converting t statistics to p values, are not covered.
I plan to take this book to work and leave it someplace where my co-workers will steal it and, hopefully, read it.
feb 13, 2016; updated feb 14, 2016
Reviewed by T. Nelson
I once got an industry scientist mad at me for suggesting that he use the Student's t-test. He was unaware that ‘Student’ was not a simplified test for students, but the pseudonym of the statistician, W.S. Gosset, who invented it. If that guy had read this book it would have made my life easier.
Thanks to computers, we take statistics for granted today. But they were great intellectual achievements, and sometimes controversial: the idea of getting a more accurate answer by throwing away information took a lot of convincing. Sometimes it's still disputed today.
Stigler's ‘seven pillars’ may sound like a typical clickbait title, but his goal is to divide the history of statistics into easy to remember categories. Laymen will learn some of the basic ideas in statistics. Scientists and mathematicians will get some interesting anecdotes.
For example, under ‘design’ he shows Ladislaus von Bortkiewicz's famous table showing the number of Prussian cavalry who got kicked to death by their horses between 1875 and 1894. This might sound silly, but it was a big problem in those days, and the table is a classic in data analysis.
Under ‘intercomparison’ he shows how time series often led people astray, like William Stanley Jevons, who thought he saw a correlation between the 11-year sunspot cycle and the business cycle. And under ‘residual’ he debunks the common myth that Florence Nightingale invented the pie chart. She did not: pie charts were William Farr's idea, though hers were indisputably nicer.
Statistically, women are much better at making pie-shaped things.
nov 08, 2016
Reviewed by T. Nelson
R is the statistics package that I prefer. It doesn't do everything, but it is powerful and accurate, it's free, it works over a telnet connection, and most importantly, it actually compiles!
But it is a command-line program, which means you have to know what tests you want to use and what the syntax is, or it just sits there looking like MS-DOS. You also have to type the data on the command line by hand. If you use big data sets, that's really inconvenient. I wrote a function from my graphical statistics spreadsheet program to output my data in R format, and many people will find large datasets too clumsy to work with in R without such a tool.
We R users don't ask for much: only a list of what commands are available, their syntax, some examples, and maybe a clear description of what the results mean. This reference book exceeds those admittedly modest expectations, and indeed the descriptions are sometimes too clear: a mention of limitations, restrictions, and alternatives would have been nice. It's far superior to searching on the Internet, where you often find an answer that doesn't work because the dorkface who wrote it was actually thinking about Stata or SAS. The only deficiency in this book is that it doesn't cover extra libraries, of which there are many (at CRAN).
I have several books on R, and this is the one that comes closest to being the reference manual. If you know what statistic you want, you look it up in the index to find the syntax. The R commands are highlighted in red and the output in blue, making them easy to find. If you want to program R, or if you want to learn statistics, or if you want 100% error-free content, look elsewhere. But if it's in the base package of R, it is probably in this book. And if you need something to whack somebody over the head with during a heated argument about statistics, thereby winning the argument, this 1000-page book is perfect. This is how science progresses.
feb 13, 2016
Disclaimer: I did not read this book in its entirety.
Reviewed by T. Nelson
R isn't only for statistics; it can also do mathematical calculations. It's a complete programming language with its own unique syntax. The packages it uses are pretty much the same as the ones described in Numerical Recipes in Fortran, to which the author frequently refers. You get linear equation solving, matrix functions, math functions like Bessel and gamma functions, numerical integration, optimization, differential equations, roots, nonlinear curve fitting, cluster analysis and FFTs.
Bloomfield sees R as a high-level language. There are no worries about declaring variables or allocating memory. Its syntax, while simple, is strict because it interprets each statement as a command. But it's not like Mathematica: its capacity for symbolic math is rudimentary. R is more like a toolbox.
The tutorials are done by example, with no theory. The main drawback in this book is that many things are used before they're described. For example, importing data is not discussed until page 273. The ‘$’ operator is first used on page 29 but not defined until page 275. The ‘%*%’ operator (matrix multiplication) is first used on page 19 but never defined at all, and many of the R options are used but never defined. You're supposed to use R's help function for all this. But you might ask: in that case, what do you need the book for?
The answer is that you need it to learn what packages and functions are available, and you get a little bit of test data to verify that they work. And that's valuable.
But I suspect the programming tutorial would be too perplexing for someone with
no exposure to computer programming. Here is the description of the
switch function on page 66:
> x = rnorm(10, 2, 0.5)
> y = 3
> switch(y, mean(x), median(x), sd(x))
[1] 0.476892
Now that's what I call cryptic. But if you're familiar with programming,
you'll realize it's just like the computed GOTO in Fortran 77—evidence of R's
roots. Even some of R's source code is still in Fortran, and you need an F77
compiler to build it.
feb 28, 2016; updated mar 05, 2016